Simple FCS example¶

This notebook shows howto compute and fit an FCS curve using pycorrelate.

Initial imports¶

In [1]:

import numpy as np
import h5py

In [2]:

# Tweak here matplotlib style
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.sans-serif'].insert(0, 'Arial')
mpl.rcParams['font.size'] = 14

In [3]:

import pycorrelate as pyc
pyc.__version__

Out[3]:

'0.3'

In [4]:

import lmfit
lmfit.__version__

Out[4]:

'0.9.7'

Load Data¶

We start downloading a sample dataset of a smFRET “measurement” with a single CW excitation laser and two detectors donor (D) and acceptor (A) (the data is actually a simulation performed with PyBroMo).

In [5]:

url = 'http://files.figshare.com/4917046/smFRET_44f3da_P_20_s0_20_s20_D_6.0e11_6.0e11_E_75_30_EmTot_200k_200k_BgD1500_BgA800_t_max_600s.hdf5'
pyc.utils.download_file(url, save_dir='data')

URL:  http://files.figshare.com/4917046/smFRET_44f3da_P_20_s0_20_s20_D_6.0e11_6.0e11_E_75_30_EmTot_200k_200k_BgD1500_BgA800_t_max_600s.hdf5
File: smFRET_44f3da_P_20_s0_20_s20_D_6.0e11_6.0e11_E_75_30_EmTot_200k_200k_BgD1500_BgA800_t_max_600s.hdf5

Downloaded  4.4 /  4.4 MB

In [6]:

fname = './data/' + url.split('/')[-1]
h5 = h5py.File(fname)
unit = h5['photon_data']['timestamps_specs']['timestamps_unit'][()]
unit

Out[6]:

4.9999999999999998e-08

We can check that there are only two detectors:

In [7]:

np.unique(h5['photon_data']['detectors'][:])

Out[7]:

array([0, 1], dtype=uint8)

Then load the timestamps in two arrays t and u:

In [8]:

detectors = h5['photon_data']['detectors'][:]
timestamps = h5['photon_data']['timestamps'][:]
t = timestamps[detectors == 0]
u = timestamps[detectors == 1]

In [9]:

t.shape, u.shape, t[0], u[0]

Out[9]:

((1152331,), (755468,), 50, 128800)

In [10]:

t.max()*unit, u.max()*unit

Out[10]:

(599.99934099999996, 599.99989349999998)

Timestamps need to be monotonic:

In [11]:

assert (np.diff(t) >= 0).all()
assert (np.diff(u) >= 0).all()

Compute CCF¶

To avoid afterpulsing, we can compute the cross-correlation function (CCF) between D and A channels.

We first create the lag bins array with the make_loglags() function:

In [12]:

# compute lags in sec. then convert to timestamp units
bins_per_dec = 20
bins = pyc.make_loglags(-6, 1, bins_per_dec)[bins_per_dec // 2:] / unit

Then, we compute the cross-correlation with pcorrelate:

In [13]:

Gn = pyc.pcorrelate(t, u, bins, normalize=True)

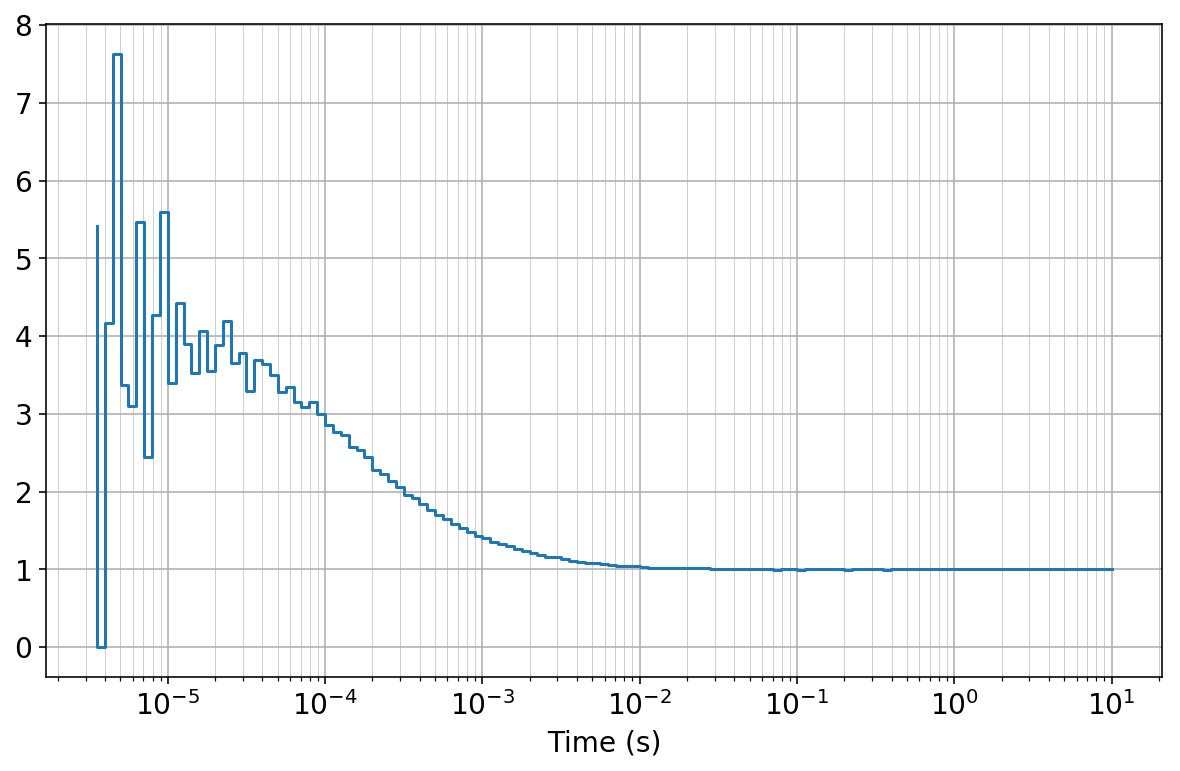
Plotting the CCF function Gn we observe the typical diffusion shape:

In [14]:

fig, ax = plt.subplots(figsize=(10, 6))
plt.semilogx(bins[1:]*unit, Gn, drawstyle='steps-pre')
plt.xlabel('Time (s)')
plt.grid(True); plt.grid(True, which='minor', lw=0.3);

../_images/notebooks_Simple_FCS_example_21_0.png

Fit FCS model¶

The next step is fitting the computed CCF with a model. For freely-diffusing species under confocal excitation (and no photo-physics) the simplest model is the 2D model (i.e. the PSF z dimension is neglected):

\[G(\tau) = 1 + A_0 \, \left(1 + \frac{\tau}{\tau_D} \right)^{-1}\]

The full 3D model is just slightly more complicated:

\[G(\tau) = 1 + A_0 \, \left(1 + \frac{\tau}{\tau_D} \right)^{-1} \; \left[ 1 + \left(\frac{r}{z}\right)^2\frac{\tau}{\tau_D} \right]^{-1/2}\]

There is a link between \(A_0\) and concentration. Neglecting background, \(A_0 = 1/N\) where \(N\) is the mean number of molecules in the excitation volume. The background makes \(A_0 < 1/N\). For full expression see Orrit 2002.

Here, for the sake of the example, we will just fit the simple 2D model.

Let’s start defining the model functions and the array of time-lags:

In [15]:

def diffusion_2d(timelag, tau_diff, A0):
    return 1 + A0 * 1/(1 + timelag/tau_diff)

def diffusion_3d(timelag, tau_diff, A0, waist_z_ratio=0.1):
    return (1 + A0 * 1/(1 + timelag/tau_diff) *
            1/np.sqrt(1 + waist_z_ratio**2 * timelag/tau_diff))

In [16]:

tau = 0.5 * (bins[1:] + bins[:-1]) * unit

Now we build a “fitting model” with lmfit and use it to fit the CCF curve Gn:

In [17]:

model = lmfit.Model(diffusion_2d)
params = model.make_params(A0=1, tau_diff=1e-3)
params['A0'].set(min=0.01, value=1)
params['tau_diff'].set(min=1e-6, value=1e-3)
#params['waist_z_ratio'].set(value=1/6, vary=False)  # 3D model only

weights = np.ones_like(Gn)
#weights = np.log(np.sqrt(G*np.diff(bins)))  # and example of using weights
fitres = model.fit(Gn, timelag=tau, params=params, method='least_squares',
                   weights=weights)
print('\nList of fitted parameters for %s: \n' % model.name)
fitres.params.pretty_print(colwidth=10, columns=['value', 'min', 'max'])


List of fitted parameters for Model(diffusion_2d):

Name           Value        Min        Max
A0             3.219       0.01        inf
tau_diff   0.0001495      1e-06        inf

Finally, we plot fit results and residuals:

In [18]:

fig, ax = plt.subplots(2, 1, figsize=(10, 8), sharex=True,
                       gridspec_kw={'height_ratios': [3, 1]})
plt.subplots_adjust(hspace=0)
ax[0].semilogx(tau, Gn)
for a in ax:
    a.grid(True); a.grid(True, which='minor', lw=0.3)
ax[0].plot(tau, fitres.best_fit)
ax[1].plot(tau, fitres.residual*weights, 'k')
ym = np.abs(fitres.residual*weights).max()
ax[1].set_ylim(-ym, ym)
ax[1].set_xlim(bins[0]*unit, bins[-1]*unit);
tau_diff_us = fitres.values['tau_diff'] * 1e6
msg = ((r'$G(0)-1$ = {A0:.2f}'+'\n'+r'$\tau_D$ = {tau_diff_us:.0f} μs')
       .format(A0=fitres.values['A0'], tau_diff_us=tau_diff_us))
ax[0].text(.75, .9, msg,
           va='top', ha='left', transform=ax[0].transAxes, fontsize=18);
ax[0].set_ylabel('G(τ)')
ax[1].set_ylabel('residuals')
ax[0].set_title('Donor-Acceptor CCF')
ax[1].set_xlabel('Time Lag, τ (s)');

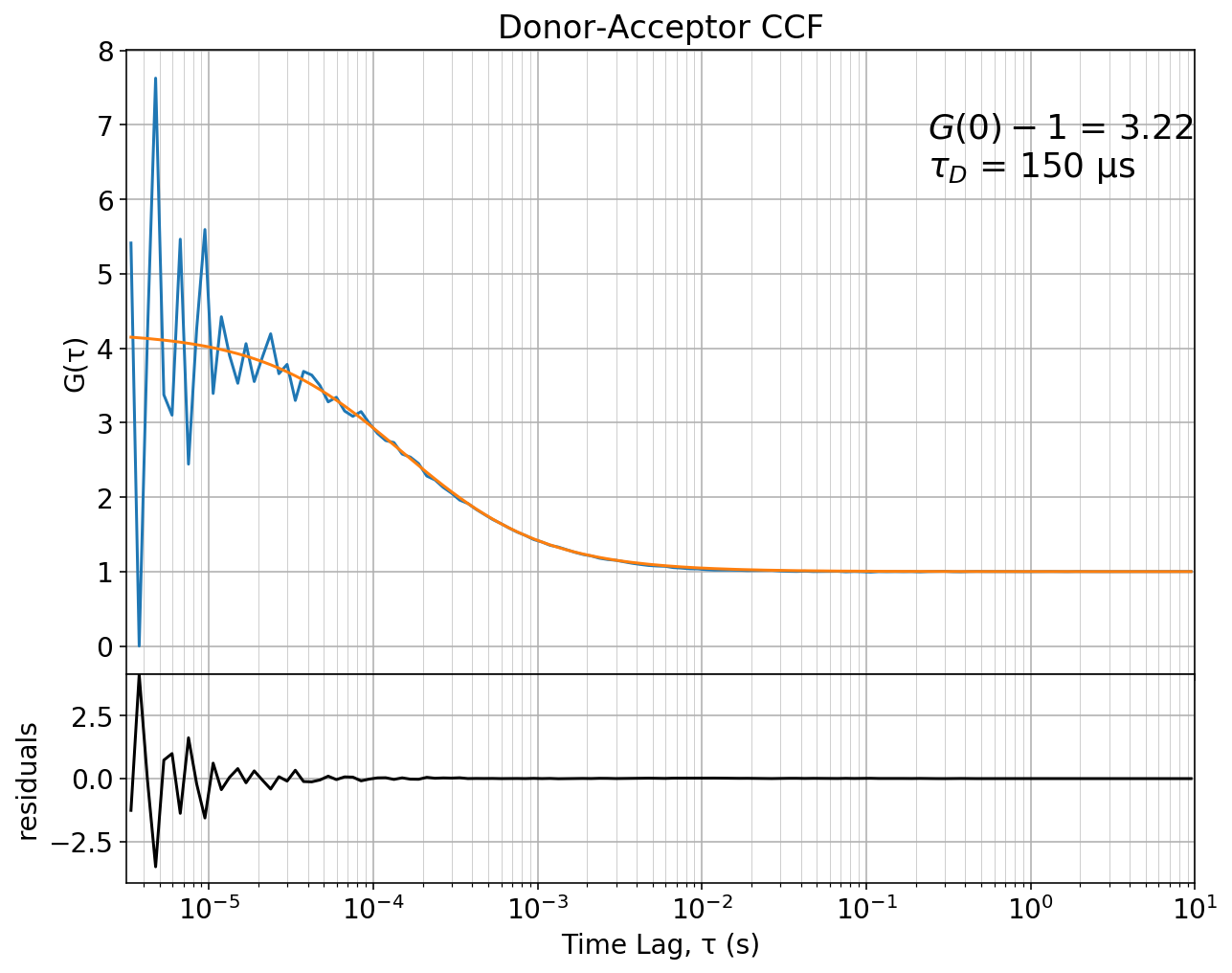
../_images/notebooks_Simple_FCS_example_28_0.png

The flatness of the residual indicates a good fit. If you followed so far, you should be able to extent this example to use more complex models when needed.